A Twitter szociális platformja hálózatelemzési szempontból aszimmetrikus, hiszen kapcsolatai szándékosak és irányítottak. Egy felhasználó kapcsolatait szociális gráfként értelmezve a címzett felé mutató nyilak követésével sok hasznos információkhoz juthatunk: ki tud kiről, ki kapja a legtöbb figyelmet, ki vesz részt bizonyos témákról folyó diskurzusokban, illetve azt is, hogy ki található centrális vagy periférián lévő pozícióban. A strukturális elemzések mellett mini-kísérletek is lebonyolíthatóak. Az ún. Tweetchat-ek keretein belül különböző témákról zajlanak egy egyórás beszélgetések, amelyek speciális hashtageken keresztül követhetőek. Az ábrákon látható beszélgetés például a szerencsés véletlenekről folyt, két különböző csoportban (#innochat, #ideachat).

Elsőként vegyük a kimenő kapcsolatokat. A Twitter természetéből kifolyólag ezek a kapcsolatok közvetítő funkciókat is betölthetnek, például ha a felhasználó bejelent valami a követőinek. Egy másik típus a közvetlen, irányított kapcsolat, amikor a felhasználó konkrétan említ valakit a tweetben, vagy re-tweeteli valaki más tweetjét. A re-tweet közvetítő funkciója mellett egyben visszaigazolás is az eredeti tweetelőnek, hogy üzenetét észlelték, és továbbításra érdemesnek találták.

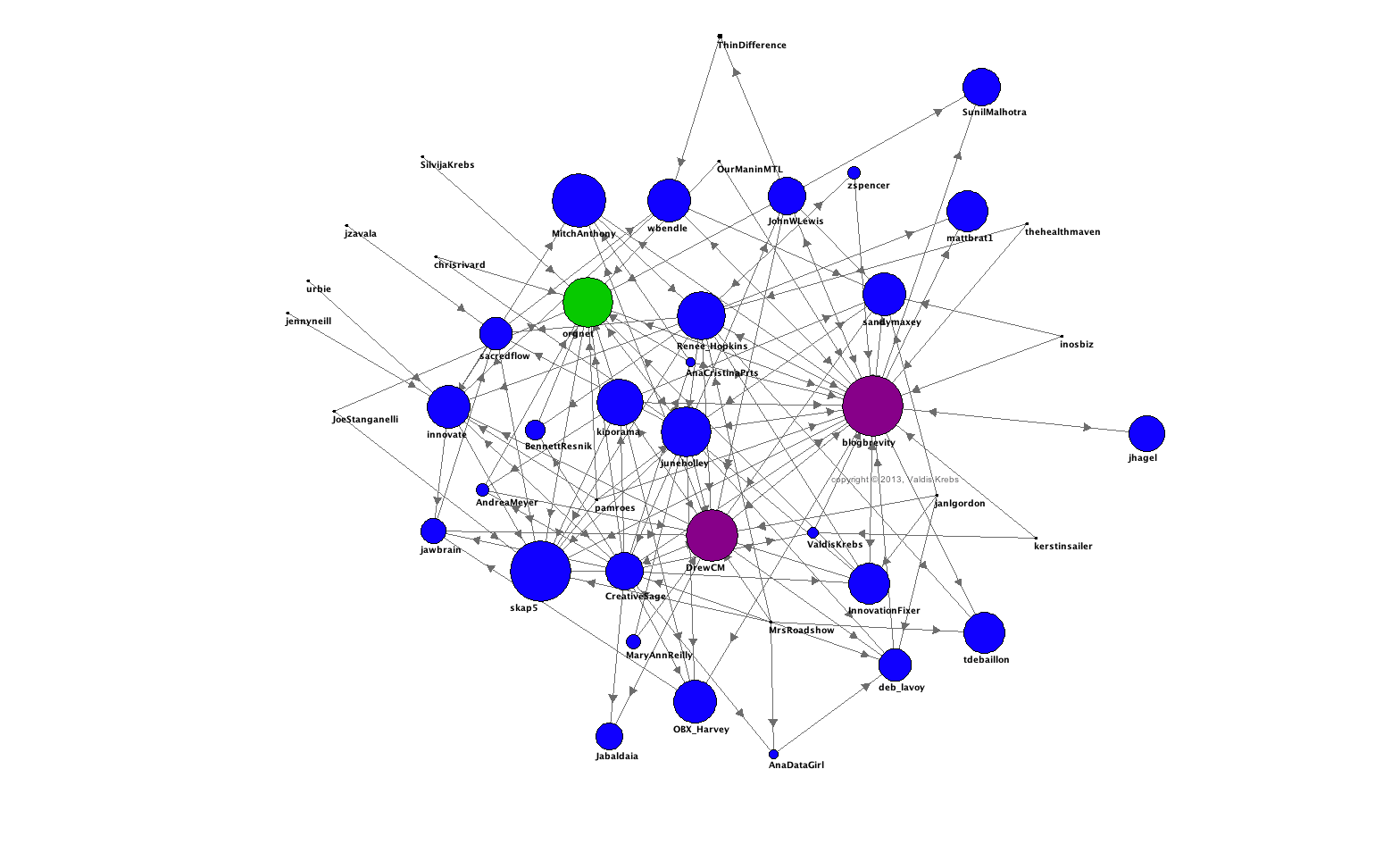
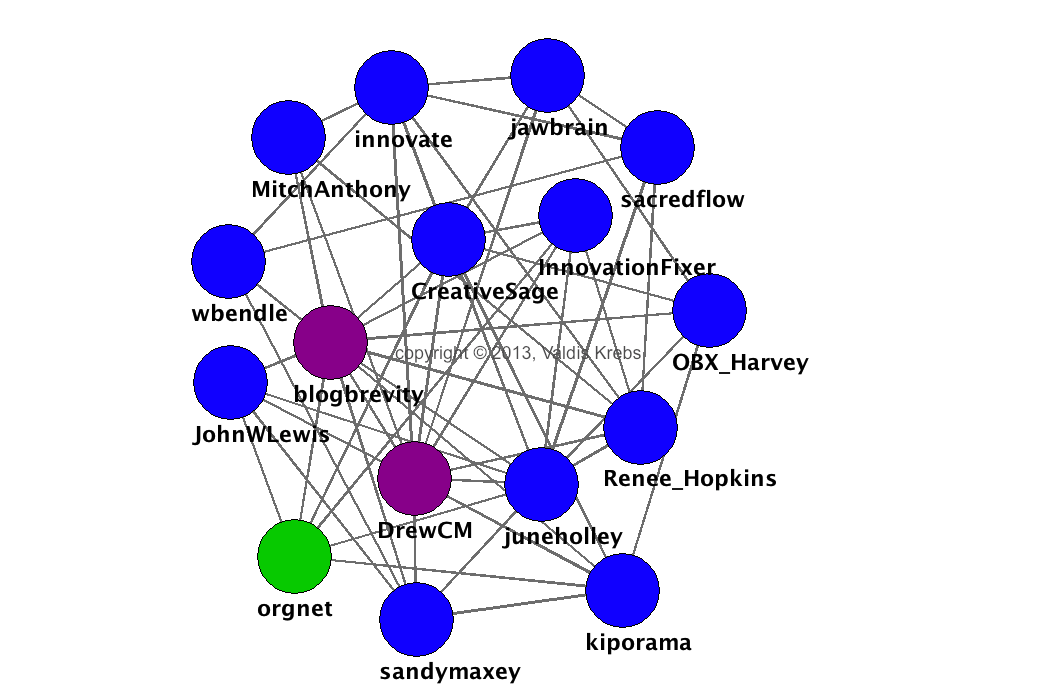
A fenti hálózat a már említett szerencsés véletlenekről szóló beszélgetés leképezése. Két pont akkor áll kapcsolatban, ha a feladó pont retweetelte (RT), említette (MT) vagy megszólította (@) a címzettet jelző pontot. A kék pontok a beszélgetés résztvevői, a lilák a chat lebonyolítói, a zöldek pedig a meghívott vendégek, mindegyikük felhasználóneve külön is fel van tüntetve. A pontok mérete itt a tudatosság mentén nő, amit a direkt és indirekt kapcsolatok alapján számolnak.

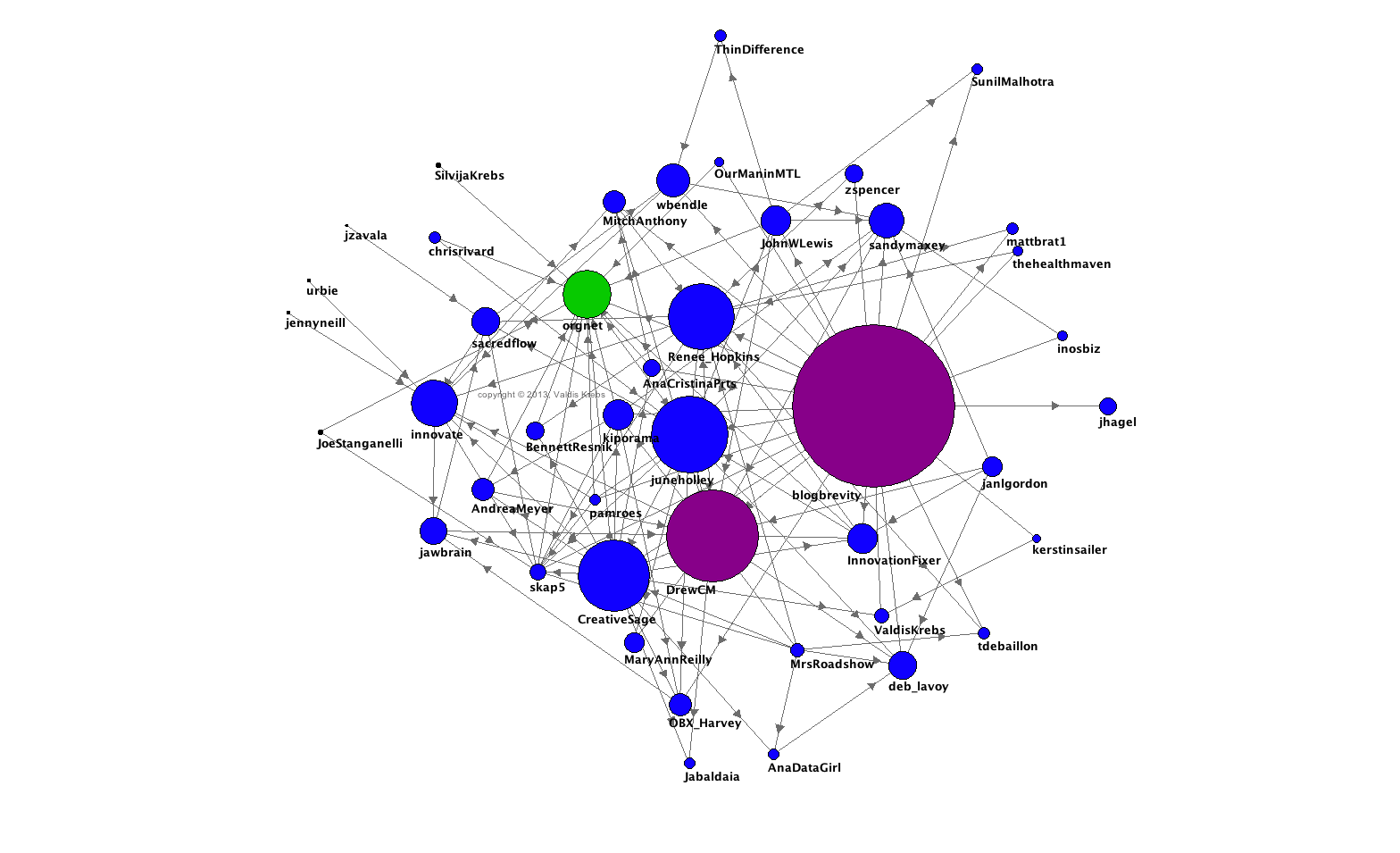
A második képen az előző hálózat látható, de a pontok méretét ezúttal kizárólag a bejövő kapcsolatok alapján határozták meg, ami gyakorlatilag nem más, mint a figyelem mennyisége, amiben az egyes felhasználók részesültek. Előnyös, ha valamelyik felhasználónak sok bejövő kapcsolata van, ami még jobb azonban, ha olyan más pontoktól kap közvetlen figyelmet, akiknek szintén sok bejövő kapcsolata van. A látványos bejövő mintázatú pontok lesznek az ún. mavenek, azaz információbrókerek.

Azzal, hogy változott a pontok méretét meghatározó tulajdonság, máris meghatározhatóak a Twitteren betöltött szerepek: vannak aktív résztvevők, míg mások arra várnak, hogy közvetlen megszólítást kapjanak. A chat vezetőjét (@blogbrevity) mindkét hálózatban nagy pont reprezentálja, ami azt mutatja, hogy jól végezte a dolgát.

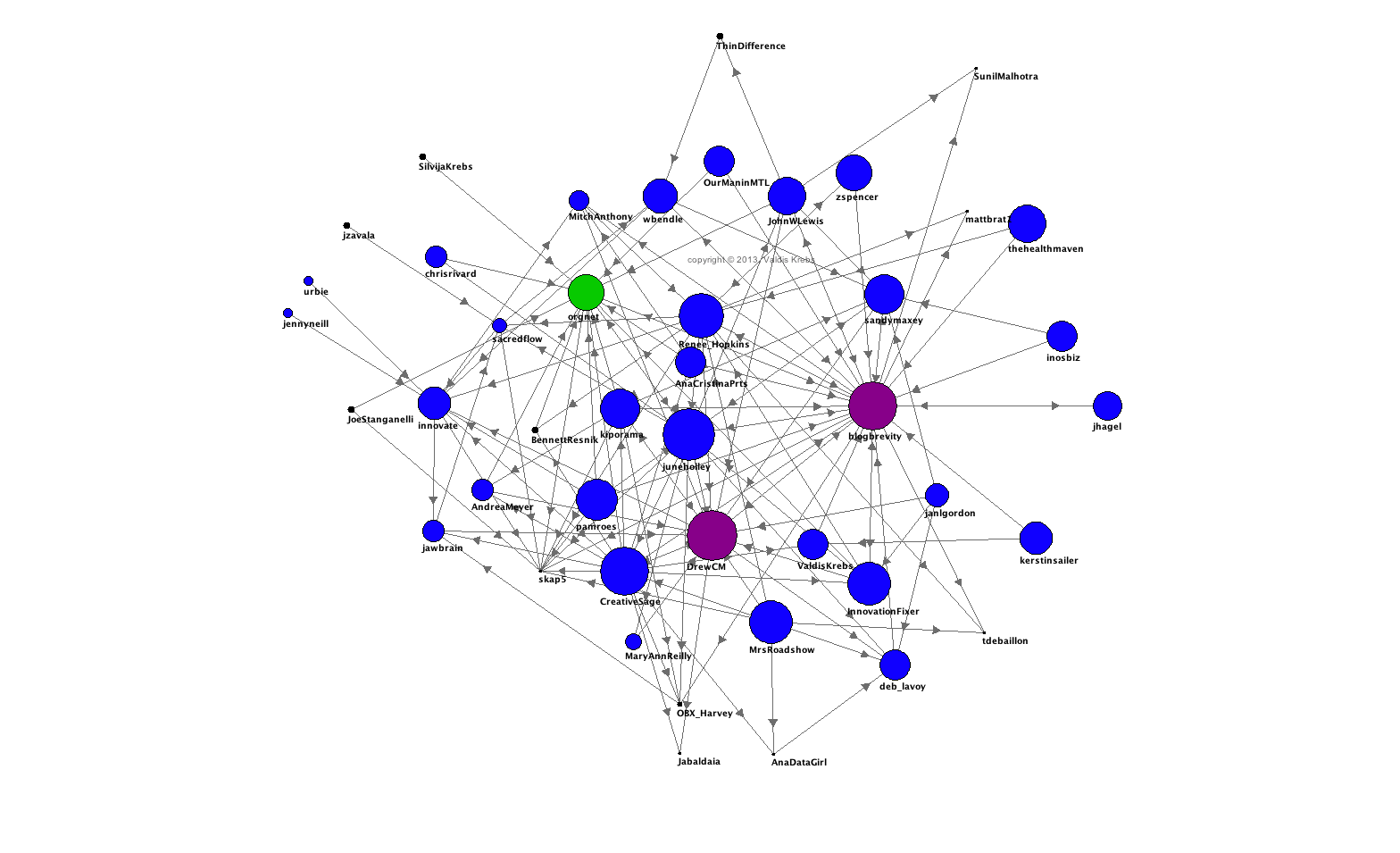
A harmadik hálózat az integrációt vizsgálja, vagyis azt, hogy az adott felhasználó mennyire van az események „ sűrűjében”. Egy jól integrált felhasználó valószínűleg releváns dolgokról tweetel, sokszor rewteetelik, és több beszélgetésben is részt vesz. Esetünkben ők voltak a szervezők, akik összekötő szerepet töltöttek be, és biztosították a beszélgetés zavartalan folyását.

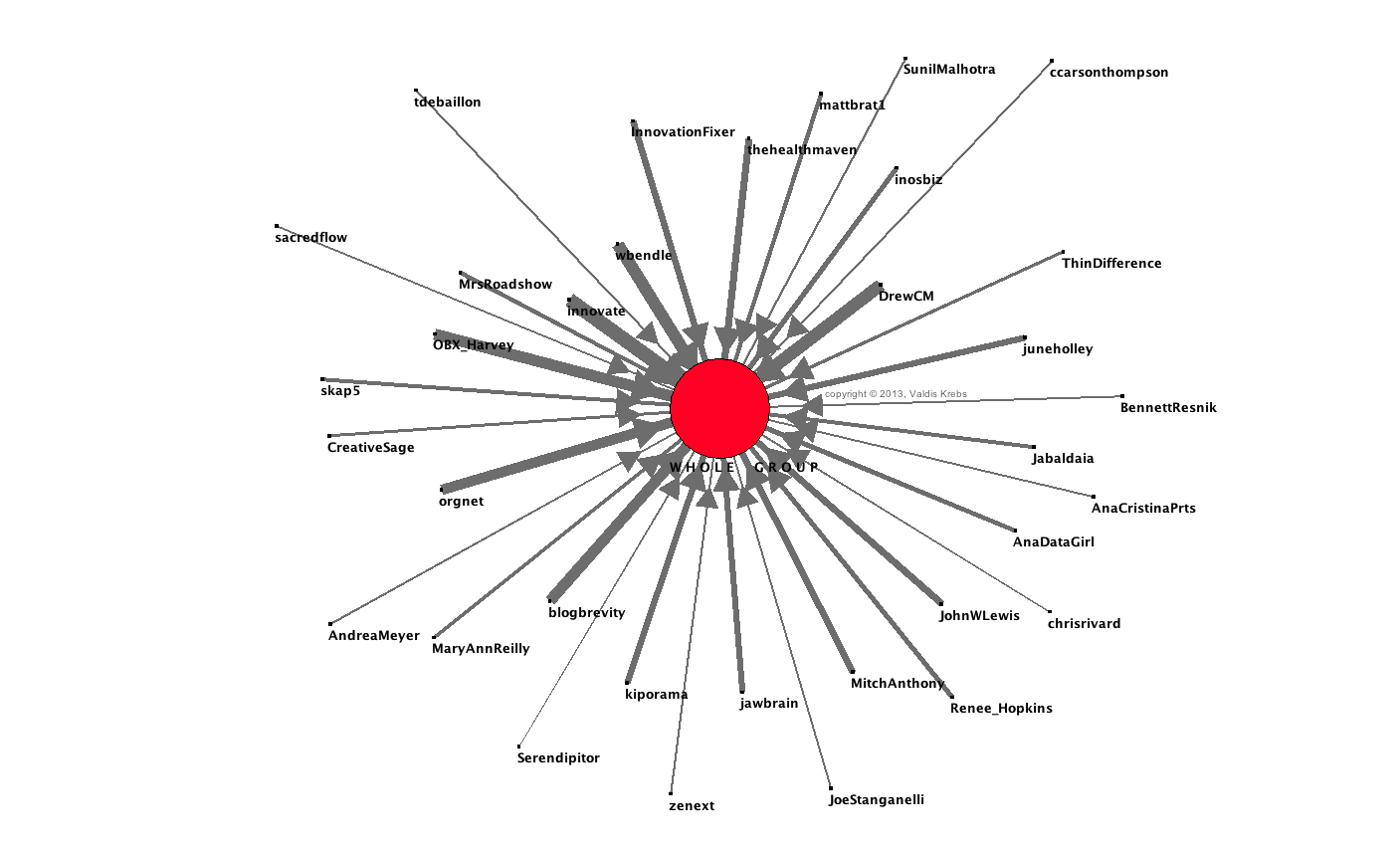
A Twitter természetesen nemcsak a személyközi kommunikáció médiuma, gyakran közvetít nagyobb csoportoknak, amiket egy felhasználó vagy egy hashtag követői alkothatnak. A chatben postolt tweetek között sok olyan is volt, aminek nem volt konkrét címzettje. A negyedik kép abban tér el az előzőektől, hogy csak az egész csoportnak szóló tweeteket mutatja, nem az interakciókat. A chat valamennyi résztvevőjét a középpontban lévő piros pont jelöli, a küllőszerű nyúlványok pedig azok a felhasználók, akiknek több mint egy, mindenkihez szóló retweetje volt. A vonalak a retweetek számának növekedésével vastagodnak.

Bár ez a hálózat pár óra leforgása alatt jött létre és oszlott fel, jól modellezi a nagyobb hálózatok néhány szerkezeti sajátosságát: centrum-periféria, információs brókerek, összekötő hidak és vezérek. A részvevők nagy része már ismerte egymást, és részt vett korábbi beszélgetésekben, volt azonban pár új tag is.

A legkönnyebben azonosítható csoport mindig a mag, akik között sűrű az egymásra mutató nyilak száma. Ez egy olyan alhálózat, ahol mindenki kapcsolatban van mindenkivel. Az ötödik kép ezt a magot mutatja, a könnyebb olvashatóság érdekében ezúttal nyilak nélkül. Minden pont legkevesebb 4 kapcsolattal rendelkezik, kimenővel és bejövővel egyaránt.

forrás: http://www.thenetworkthinkers.com/2013/02/arrows-on-twitter.html