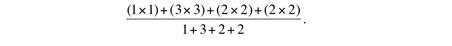Az első ránézésre szociális jelenség mögött alapvető aritmetikai törvényszerűség áll.
Johan Ugander, Brian Karrer, Lars Backstrom és Cameron Marlow egy nagy volumenű kutatás során tesztelték a jelenséget a Facebook (akkori) összes felhasználójával (!), mintegy 721 millió emberen, ami a Föld népességének 10%-át tesz ki. A 69 milliárd kapcsolat elemzése után azt tapasztalták, hogy a paradoxon az esetek 93%-ban megvalósul. Az átlagfelhasználó 190 baráttal rendelkezik, míg az átlagfelhasználó átlagbarátja 635-el.
A jelenség offline hálózatok esetén is tapasztalható, és teljes mértékben független az adott ember személyiségétől, és nem véletlenül a barátság paradoxon néven híresült el. A paradoxon forrása a súlyozott átlag, a dolog lényege pedig, hogy egy szám kétszer szerepel, egyszer átlagoljuk, egyszer súlyként. Vegyünk egy kisebb hálózatot példának (a jelenség egyébként független a hálózat szerkezetétől, a méret a szemléltetés érthetőségét szolgálja).
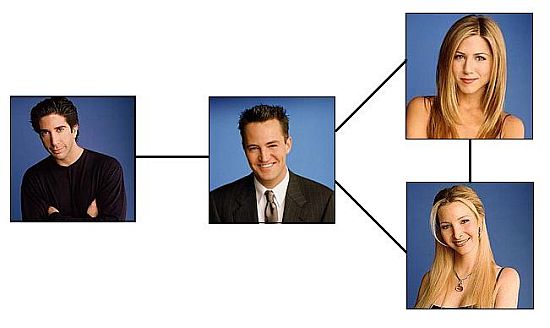
Ross, Chandler, Rachel és Phoebe (jó)barátok. Ross Chandler barátja, utóbbi pedig közkedvelt személyiség sok baráttal. Rachel és Phoebe is barátok, és mindketten ismerik Chandlert. Rossnak tehát 1, Chandlernek 3, Rachelnek és Phoebenek pedig 2 barátja van. Összesen tehát 8 barát van, a 4 embernek átlagosan 2. A barátság paradoxonban ez a 2-es átlag az a szám, aminek kisebb, mint a barátok barátainak átlagos száma (a továbbiakban rang). Valóban így van ez?
Lássuk az egyes emberek átlagos rangját: Rossnak 1, Chandlernek 3, Phoebynek és Rachelnek 2. Képzeljünk el egy beszélgetést, ahol a barátok egymással beszélnek rangjaikról:
Ross: “Chandler rangja 3.”
Chandler: “Ross rangja 1. Rachel rangja 2. Phoebé pedig 2.”
Rachel: “Chandler rangja, Phoebe rangja 2.”
Phoebe: “Chandler rangja 3. Rachel rangja 2.”
A rangok összege 18 (3 + 1 + 2 + 2 + 3 + 2 + 3 + 2), nyolccal elosztva az átlaga pedig 2.25, ami bizony magasabb, mint 2. A paradoxonnak megfelelően tehát a barátok barátainak száma magasabb, mint a saját barátoké. A kérdés már csak az, miért? A populáris barátok, mint Chandler aránytalanul magasabb rangúak, mint az átlag, és azon felül hogy sok barátjuk van, őket is sokszor említik barátként. A fenti képletben Rosst egyszer említették, így ő 1x1-et ad hozzá; Chandler neve háromszor merült fel, rangja 3, tehát 3x3=9; Rachel és Phoebe két-két említése pedig 2x2, így a rangok átlaga (fent), nagyobb, mint a barátok tálaga (lent), a felső ezzel súlyozott átlag lesz, a négyzetre emelés így extra súlyt ad a nagy ranghoz.
Az átlagolt rang így mindig magasabb lesz, mint a sima átlag, ami nincs súlyozva.
A paradoxonnak nem meglepő módon gyakorlati alkalmazása is létezik, többek között egy járványok elterjedését megelőzni szándékozó figyelmeztető rendszer. A 2009-es H1N1 vírus kitörésekor egy Harvardon folytatott kísérlet azt is kimutatta, hogy a Chandler kaliberű, sok ismerőssel rendelkező diákok előbb megbetegedtek.
További példákkal a New York Times egyik blogja szolgál.